Autor prezentacji: Pan dr Ryszard Stagraczyński
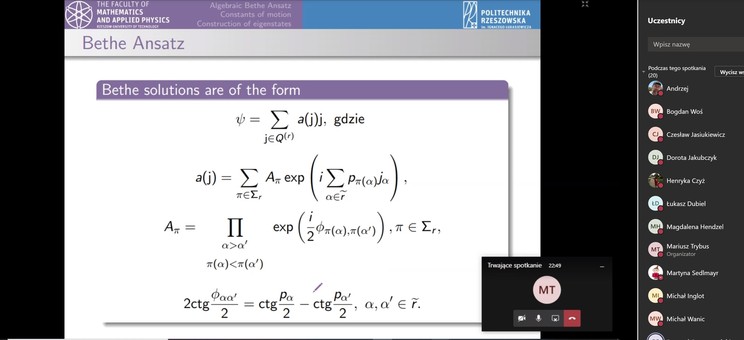
Seminarium było poświęcone analizie metod algebraicznych w zagadnieniu podstawienia Bethego (Bethe ansatz) dla jednowymiarowego układu cząstek posiadających spin. Tego typu łańcuchy stanowią rodzaj układu wielu ciał, dla których można znaleźć ścisłe rozwiązania zagadnienia własnego. Jest to powód, dla którego metody obliczeniowe stosowane przy podejściu Bethego znajdują zastosowanie w wielu aspektach fizyki matematycznej i informatyki.
Wykorzystanie podstawienia Bethego dotyczy rozwiązania zagadnienia własnego w modelu magnetyka mającego postać łańcucha złożonego z wielu węzłów, z których każdy obsadzony jest spinem ½. Dr Stagraczyński omówił metodę opisu układu poprzez analizę hamiltonianu zawierającego operatory działające na wybranym węźle. Jednym z przypadków wykorzystujących ten typ hamiltonianu jest model Heisenberga dla łańcucha XXX z jednakową postacią całek wymiany. Metodę tę można zastosować także do modelu Hubbarda.
Każdy dwuciałowy sektor łańcucha posiada w podejściu Bethego nietrywialną macierz rozpraszania, zależną od pędów. Ponadto funkcja falowa układu wielu ciał jest zależna od funkcji falowej układów dwuciałowych. W rozwiązaniach brzegowych modelu Heisenberga uwzględnia się wyrazy opisujące rozpraszanie solitonowe, gdzie wymiana pędu między cząstkami odbywa się bez zmiany jego wartości. Podstawienie Bethego stanowi sposób na uwzględnienie obsadzenia węzłów z wykluczeniem podwójnych obsadzeń. W rezultacie możliwy staje się opis układu bez konieczności stosowania dodatkowych warunków wykluczających. W celu otrzymania rozwiązań wykorzystuje się parametry spektralne, spełniające równanie, które mimo złożoności rozwiązań posiada bardzo przejrzystą formę.
Stopień komplikacji problemu rośnie wraz ze wzrostem liczby parametrów w przypadku większej liczby węzłów i cząstek. Przy rozwiązywaniu zagadnienia własnego istotne jest uzyskanie wyników jednoznacznych i wyrażonych przy pomocy odpowiedniej liczby funkcji falowych; dla modelu XXX problem ten nadal jest kwestią otwartą. Jednym ze sposobów jego rozwiązania jest metoda stosowana przez grupę Faddeeva z wykorzystaniem formalizmu operatorów drabinkowych. W ramach tego ujęcia przeprowadza się konstrukcje operatorów działających efektywnie w przestrzeni magnetyka. W tym celu traktujemy je jak funkcje, na które działamy operatorami drabinkowymi. Pan Dr przedstawił sposób zapewnienia użyteczności metody w oparciu o równanie Yanga-Baxtera. Metoda ta opiera się na konstrukcji klasy rozwiązań równoważnych dla modeli całkowalnych. Omówiony został sposób uwzględnienia oddziaływania na siebie sąsiadujących spinów oraz metody wykorzystania operatorów wagowych, określających liczbę możliwych kombinacji spinów. Zarówno operatory wagowe jak i drabinkowe można dopasować w ten sposób aby otrzymać zgodność z podstawieniem Bethego.
Jednym ze sposobów przejścia od lokalnych zmiennych dynamicznych do problemu całkowego jest tzw. macierz monodromii. Stanowi ona rodzaj uporządkowanego iloczynu operatorów, zaś jej ślad pozwala na uzyskanie całek ruchu. W prezentacji zostały omówione wyniki działania operatorów przełączania spinu na węzłach łańcucha oraz warunków otrzymania stanów własnych hamiltonianu. Przedstawiono także efekt działania na dany stan macierzą transferu, która w zależności od parametrów spektralnych prowadzi do różnych współczynników. Przyjęcie, iż niektóre z tych współczynników są równe zeru pozwala odtworzyć fizyczny model równoważny podstawieniu Bethego.
Innym sposobem jest metoda całek ruchu, gdzie macierz transferu ma postać wielomianową, zaś dowolny stan możemy konstruować przy pomocy operatorów rzutowania na wartości własne konkretnych operatorów. Pan Dr zaprezentował przykład rozwiązań otrzymanych dla cyklicznego łańcucha złożonego z pięciu węzłów. Omówił również metodę konstrukcji macierzy monodromii poprzez wykorzystanie elementów, których sekwencja ma postać słów w alfabecie operatorów. Dobór kolejności liter takiego słowa musi być zgodny z regułami mnożenia macierzy. Niektóre z tych słów mają postać ciągłych ścieżek pozwalających na uzyskanie elementów macierzy. Jako przykład przedstawiony został opis modyfikacji stanów własnych hamiltonianu poprzez działanie operatorem zmieniającym spiny w dowolnym węźle. W rezultacie takie losowe działanie na stan własny prowadzi do przypadkowych zaburzeń parametrów spektralnych. Procedura sprowadza się wówczas do wyboru odpowiedniego stanu.